题目描述
棋盘上 $A$ 点有一个过河卒,需要走到目标 $B$ 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$,同样马的位置坐标是需要给出的。
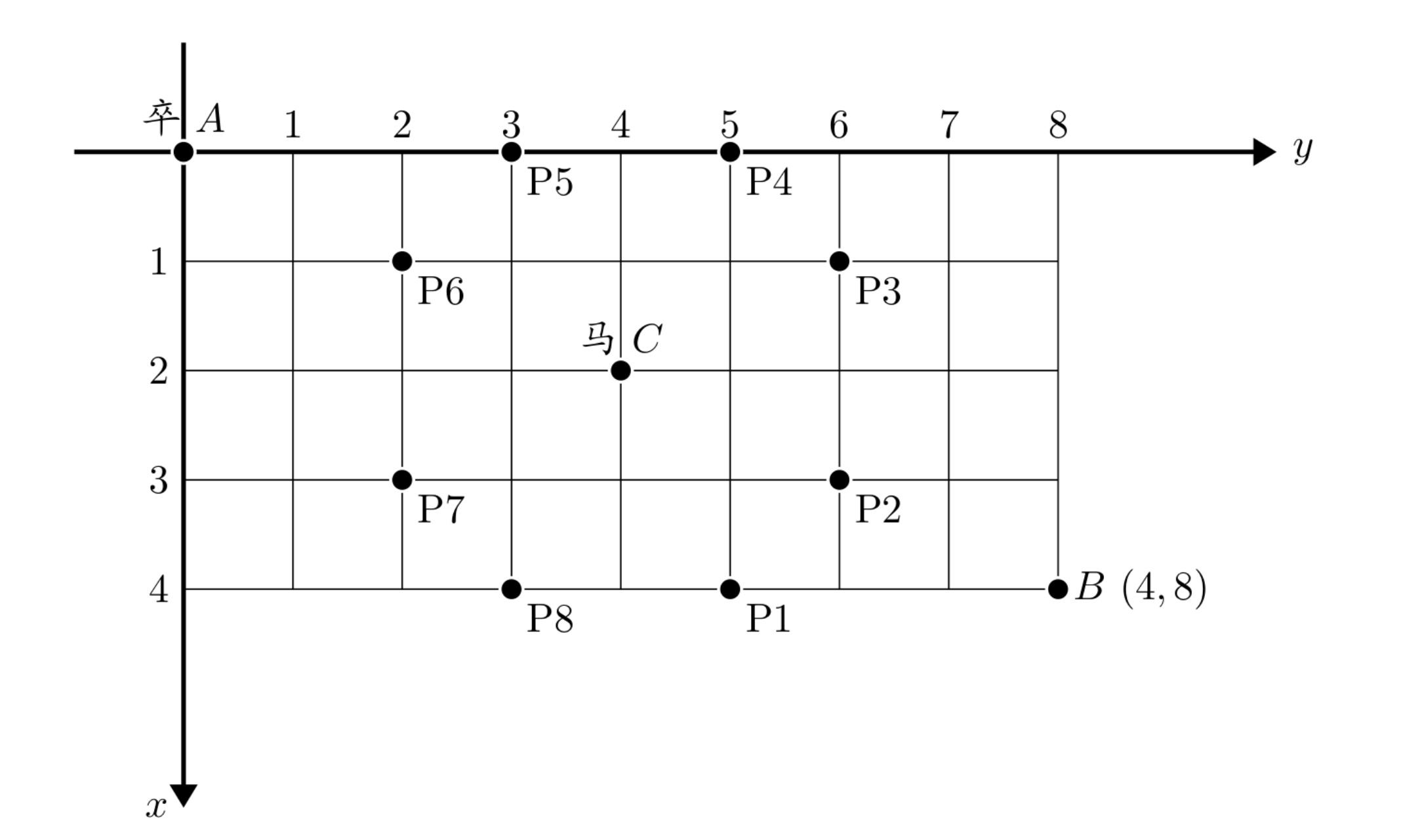
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个正整数,分别表示 $B$ 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
输入输出样例 #1
输入 #1
输出 #1
说明/提示
对于 $100 %$ 的数据,$1 \le n, m \le 20$,$0 \le$ 马的坐标 $\le 20$。
大概思路
这里我们先忽略马的控制点,只讨论卒从A点运动到B点的路径条数。
不难发现,如果B点与A点在同一条直线上,那么卒的路径就只有一条。
现在假设B点坐标为$(1,1)$,那路径是不是有两条?一个是先向下再向右,另一个是先向右再向下。
如果B点坐标为$(1,2)$,那路径有多少条?
自己画一下,是不是有三条?
B点坐标为$(2,1)$呢?
欸,这时我们可以发现一个规律:
如果B点坐标为$(x,y)$,那么卒的路径条数为他到$(x-1,y)$的路径条数加上他到$(x,y-1)$的路径条数。
有没有发现这很像我们在高中时做的数学概率题目?我们只需要每次考虑结果的上一步。
那么此时的代码应该是:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| #include <bits/stdc++.h>
using namespace std;
int main() {
long long n, m, x, y;
cin >> n >> m >> x >> y;
long long a[30][30] = {0};
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
if(i == 0 && j == 0){
continue;
}
if(i == 0 || j == 0){
a[i][j] = 1;
}
else{
a[i][j] = a[i-1][j] + a[i][j-1];
}
}
}
cout << a[n][m] << endl;
return 0;
}
|
好,下面我们再把马的控制点考虑进来
首先肯定要标记出马的控制点,我们可以先把二维数组中所有的元素都赋值为1,然后再手动把马的控制点的坐标标记为0(听起来有点苕)。
另外,要注意马的控制点是否在棋盘上面!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| long long n, m, x, y;
cin >> n >> m >> x >> y;
long long a[30][30] = {0};
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
a[i][j] = 1;
}
}
a[x][y] = 0;
if(x + 2 <= n && y - 1 >= 0){
a[x+2][y-1] = 0;
}
if(x + 2 <= n && y + 1 <= m){
a[x+2][y+1] = 0;
}
if(x - 2 >= 0 && y - 1 >= 0){
a[x-2][y-1] = 0;
}
if(x - 2 >= 0 && y + 1 <= m){
a[x-2][y+1] = 0;
}
if(x - 1 >= 0 && y - 2 >= 0){
a[x-1][y-2] = 0;
}
if(x - 1 >= 0 && y + 2 <= m){
a[x-1][y+2] = 0;
}
if(x + 1 <= n && y - 2 >= 0){
a[x+1][y-2] = 0;
}
if(x + 1 <= n && y + 2 <= m){
a[x+1][y+2] = 0;
}
|
然后在遍历数组的时候,如果数组元素为0,即遇到马的控制点,就要跳过这个点,不进行路径计数。
1
2
3
4
5
6
7
8
9
10
| for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
if(i == 0 && j == 0){
continue;
}
if(a[i][j] == 0){
continue;
}
}
}
|
我们接着用相同的方法找一下规律,
当B点在第一列或者第一行时,他的路径条数等于他的上面或者左边的路径条数。
1
2
3
4
5
6
| if(i == 0){
a[i][j] = a[i][j-1];
}
else if(j == 0){
a[i][j] = a[i-1][j];
}
|
当B点在第一列或者第一行以外时,他的路径条数等于他的上面或者左边的路径条数加上他的左上角的路径条数。
1
2
3
| else{
a[i][j] = a[i-1][j] + a[i][j-1];
}
|
完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| #include <bits/stdc++.h>
using namespace std;
int main() {
long long n, m, x, y;
cin >> n >> m >> x >> y;
long long a[30][30] = {0};
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
a[i][j] = 1;
}
}
a[x][y] = 0;
if(x + 2 <= n && y - 1 >= 0){
a[x+2][y-1] = 0;
}
if(x + 2 <= n && y + 1 <= m){
a[x+2][y+1] = 0;
}
if(x - 2 >= 0 && y - 1 >= 0){
a[x-2][y-1] = 0;
}
if(x - 2 >= 0 && y + 1 <= m){
a[x-2][y+1] = 0;
}
if(x - 1 >= 0 && y - 2 >= 0){
a[x-1][y-2] = 0;
}
if(x - 1 >= 0 && y + 2 <= m){
a[x-1][y+2] = 0;
}
if(x + 1 <= n && y - 2 >= 0){
a[x+1][y-2] = 0;
}
if(x + 1 <= n && y + 2 <= m){
a[x+1][y+2] = 0;
}
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
if(i == 0 && j == 0){
continue;
}
if(a[i][j] == 0){
continue;
}
if(i == 0){
a[i][j] = a[i][j-1];
}
else if(j == 0){
a[i][j] = a[i-1][j];
}
else{
a[i][j] = a[i-1][j] + a[i][j-1];
}
}
}
cout << a[n][m] << endl;
return 0;
}
|
